A Stabilized Finite Element Method for Modified Poisson-Nernst-Planck Equations to Determine Ion Flow Through a Nanopore
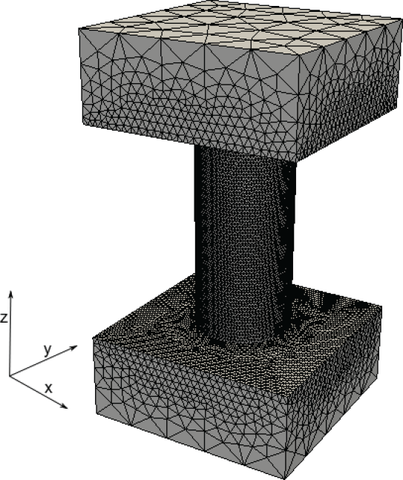
The conventional Poisson-Nernst-Planck equations do not account for the finite size of ions explicitly. This leads to solutions featuring unrealistically high ionic concentrations in the regions subject to external potentials, in particular, near highly charged surfaces. A modified form of the Poisson-Nernst-Planck equations accounts for steric effects and results in solutions with finite ion concentrations. Here, we evaluate numerical methods for solving the modified Poisson-Nernst-Planck equations by modeling electric field-driven transport of ions through a nanopore. We describe a novel, robust finite element solver that combines the applications of the Newton's method to the nonlinear Galerkin form of the equations, augmented with stabilization terms to appropriately handle the drift-diffusion processes. To make direct comparison with particle-based simulations possible, our method is specifically designed to produce solutions under periodic boundary conditions and to conserve the number of ions in the solution domain. We test our finite element solver on a set of challenging numerical experiments that include calculations of the ion distribution in a volume confined between two charged plates, calculations of the ionic current though a nanopore subject to an external electric field, and modeling the effect of a DNA molecule on the ion concentration and nanopore current.